Math behind ordinary least square approximation

In this section we will derive the equations for slope and intercept which are used in ordinary square approximation.

step 1:
  Let the data given be : (X₁, Y₁), (X₂,Y₂),...(X_n,Y_n)
  We want to fit a linear line, let that line be: Y = MX + b

step 2:
   We want to fit the line in such a way that sum of squared errors should be as low as possible
  sum of squared errors could be written as:
  SE_LINE = ( Y₁ - (MX₁ + b) )² + ( Y₂ - (MX₂ + b) )² + ......... + ( Y_n - (MX_n + b) )²
  in this equation we have to find M and b that minimises SE_LINE

step 3:
  Expanding above equation
  SE_LINE =  ( Y₁² + (MX₁ + b)² - 2*Y₁* (MX₁ + b) )
      + ( Y₂² + (MX₂ + b)² - 2*Y₂* (MX₂ + b) )
      + ( Y₃² + (MX₃ + b)² - 2*Y₃* (MX₃ + b) )
      + .......
      + ( Y_n² + (MX_n + b)² - 2*Y_n* (MX_n + b) )

  Expanding again
  SE_LINE =  ( Y₁² + MX₁² + b² + 2MX₁b - 2Y₁MX₁ -2Y₁b )
      + ( Y₂² + MX₂² + b² + 2MX₂b - 2Y₂MX₁ -2Y₂b)
      + ( Y₃² + MX₃² + b² + 2MX₃b - 2Y₃MX₁ -2Y₃b)
      + .......
      + ( Y_n² + MX_n² + b² + 2MX_nb - 2Y_nMX₁ -2Y_nb)

step 4:
  Rewriting the above equation
  SE_LINE =  ( Y₁² + Y₂² + Y₃² +..........+ Y_n² ) + M² ( X₁² + X₂² + X₃² +..........+ X_n² ) + nb²
      + 2Mb (X₁ + X₂ + X₃ +..........+ X_n) - 2M (X₁Y₁ + X₂Y₂ + X₃Y₃ +..........+ X_nY_n)
      - 2b ( Y₁ + Y₂ + Y₃ +..........+ Y_n )

step 5:

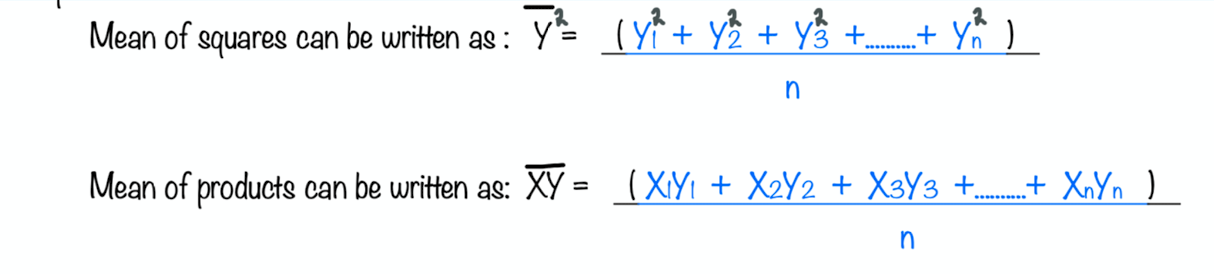
  Hence substituting similar equations on above:

  SE_LINE =  nY²  +  M²nX² +  nb²  +  2MbnX  - 2MnXY - 2bnY 

step 6:
  - So now we have simplified the equation which we want to minimise
  - If we observe the above equation carefully, for given input and actual all
   the parameters are constants except M and b
  - So for different M and b we will have different Sum of Squared Errors
  - If we do lot of observations on different M and b the graph looks like this:

  - From the above graph it is clear that Sum of squared error is minimum where we have marked star
  - This coordinate is present at that point where slope with respect M and slope with respect to b is zero.
  - Hence, we can use partial derivative to obtain this point
           d(SE_LINE)/dM = 0    d(SE_LINE)/db = 0
  - partial derivatives are used to find the slope and by assigning 0 we will know that at these points
   slope is minimum

step 7:
   Let's solve for d(SE_LINE)/dM = 0

         d(nY²  +  M²nX² +  nb²  +  2MbnX  - 2MnXY - 2bnY) /dM = 0

        (2 n X² M) + (2 b n X) - ( 2 n XY ) = 0

   Let's solve for d(SE_LINE)/db = 0

         d(nY²  +  M²nX² +  nb²  +  2MbnX  - 2MnXY - 2bnY) /db = 0

        (2 n b) + (2 M n X) - ( 2 n Y ) = 0

step 8:
   We have 2 equations from above. Those are:

        (2 n X² M) + (2 b n X) - ( 2 n XY ) = 0

        (2 n b) + (2 M n X) - ( 2 n Y ) = 0

   Dividing these 2 equations with "2n"

         X² M  +  b X - XY = 0  ................... (eq 1)

         b  +  M X - Y = 0  ................... (eq 2)

step 9:
  If we substitute second equation in first we will get:

Note: we can rewrite both of these equations in Y = MX + b format and can say that any regression line that better fits data points should have to go through ( µ_x , µ_y )