Vanishing and Exploding Gradients

Vanishing Gradient

In Adaptive Gradient optimization algorithm, learning rate plays an important role in determining the updated parameter values. Unlike Stochastic Gradient descent, this optimizer uses a different learning rate for each iteration(EPOCH) rather than using the same learning rate for determining all the parameters.

it performs smaller updates(lower learning rates) for the weights corresponding to the high-frequency features and bigger updates(higher learning rates) for the weights corresponding to the low-frequency features, which in turn helps in better performance with higher accuracy. Adagrad is well-suited for dealing with sparse data.
Important function of the optimizer is to update the weights of the learning algorithm to reach the least cost function. Here is the formula used by all the optimizers for updating the weights with a certain value of the learning rate.

So at each iteration, first the alpha at time t will be calculated and as the iterations increase the value of t increases, and thus alpha t will start increasing.

Now the learning rate is calculated at each time step. Given by,

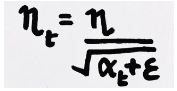
Here epsilon is a small positive number added to alpha to avoid the error if at any instance alpha becomes zero

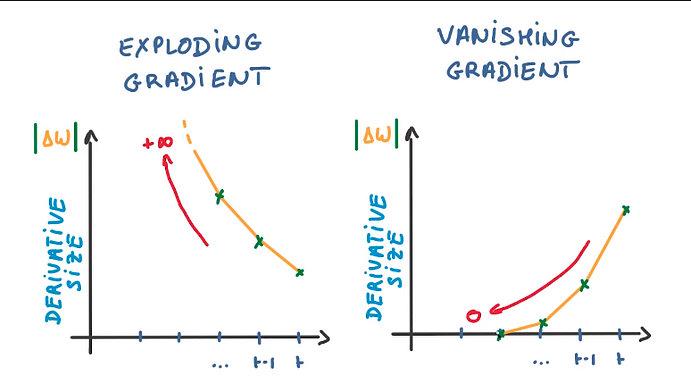
However, there is a disadvantage of getting into the problem of Vanishing Gradient because after a lot of iterations the alpha value becomes very large making the learning rate very small leading to no change between the new and the old weight. This in turn causes the learning rate to shrink and eventually become very small, where the algorithm is not able to acquire any further knowledge.

Exploding Gradient

he exploding gradient problem is another issue related to the training of deep neural networks, somewhat like the flip side of the vanishing gradient problem. This problem occurs when the gradient becomes too large, which can cause an unstable and inefficient learning process.

In detail, during backpropagation, gradients are passed back through the network. With each layer, these gradients are multiplied by the weights of the current layer. When these weights have large values or the gradients themselves are large, the result of this multiplication can be a very large gradient. When the network is deep, i.e., has many layers, these large gradients can result in very large updates to neural network model weights during training.

Handling vanishing & exploding Gradient

Mitigating the vanishing/exploding gradient problem is crucial for training deep neural networks effectively. Here are some strategies to address this issue:
    1. Proper Weight Initialization
    2. Using Activation Functions
    3. Batch Normalization
    4. Gradient Clipping using predefined threshold
    5. Skip Connections
    6. Better optimisers (= Gradient Descent Variants)