Regularization in Machine Learning

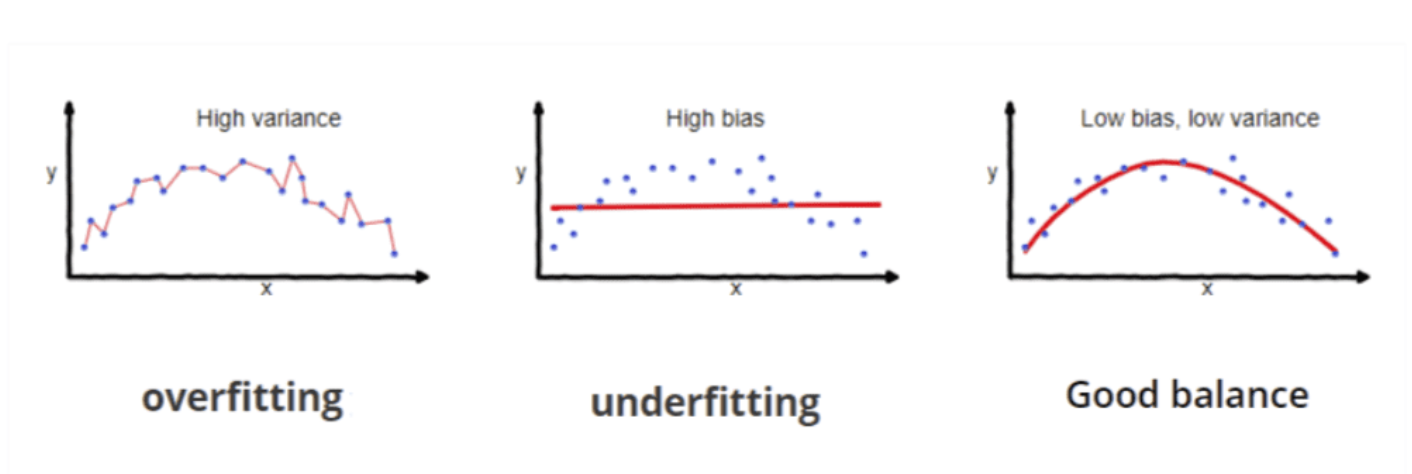
While developing machine learning models you must have encountered a situation in which the training accuracy of the model is high but the validation accuracy or the testing accuracy is low. This is the case which is popularly known as overfitting in the domain of machine learning.

In this article, we will learn about a method known as Regularization in Python which helps us to solve the problem of overfitting.

Role Of Regularization

In Python, Regularization is a technique used to prevent overfitting by adding a penalty term to the loss function, discouraging the model from assigning too much importance to individual features or coefficients.

Let’s explore some more detailed explanations about the role of Regularization in Python:
1. Complexity Control
2. Preventing Overfitting
3. Balancing Bias and Variance
4. Feature Selection: Some regularization methods, such as L1 regularization (Lasso), promote sparse solutions that drive some feature coefficients to zero. This automatically selects important features while excluding less important ones.
5. Handling Multicollinearity: When features are highly correlated (multicollinearity), regularization can stabilize the model by reducing coefficient sensitivity to small data changes.
6. Generalization: Regularized models learn underlying patterns of data for better generalization to new data, instead of memorizing specific examples.

Regularization in Machine Learning

Regularization is a technique used to reduce errors by fitting the function appropriately on the given training set and avoiding overfitting. The commonly used regularization techniques are :
    1. Lasso Regularization – L1 Regularization
    2. Ridge Regularization – L2 Regularization
    3. Elastic Net Regularization – L1 and L2 Regularization

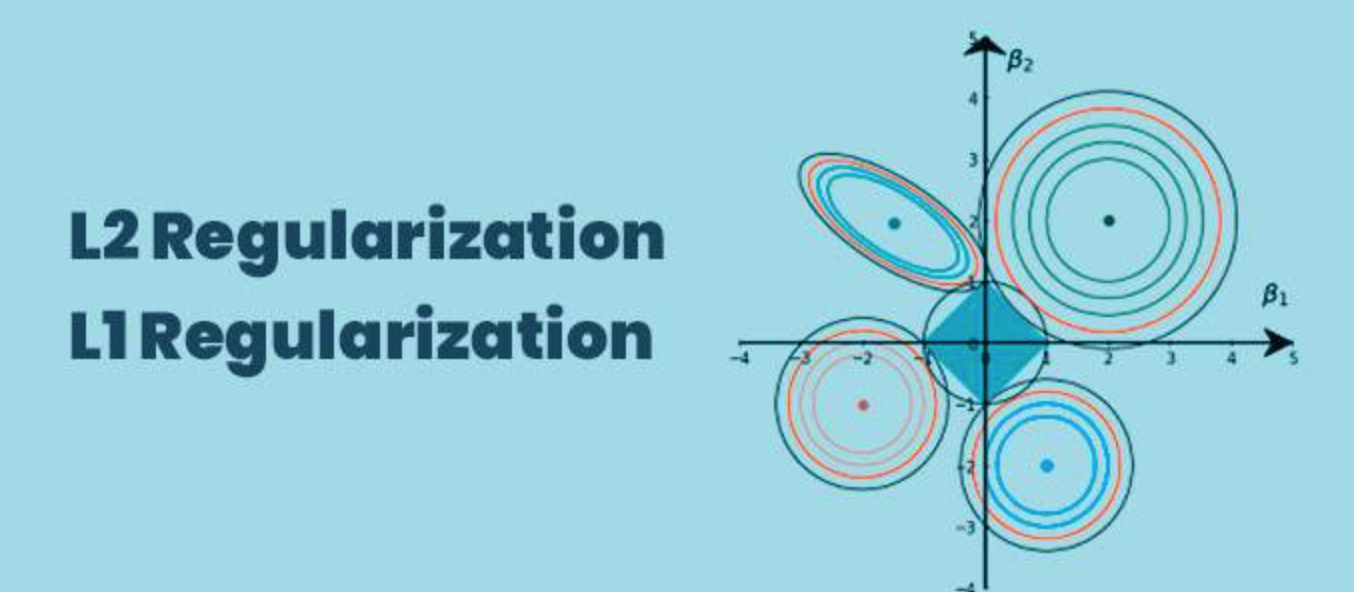
1. Lasso Regularization – L1 Regularization

A regression model which uses the L1 Regularization technique is called LASSO(Least Absolute Shrinkage and Selection Operator) regression. Lasso Regression adds the “absolute value of magnitude” of the coefficient as a penalty term to the loss function(L). Lasso regression also helps us achieve feature selection by penalizing the weights to approximately equal to zero if that feature does not serve any purpose in the model.

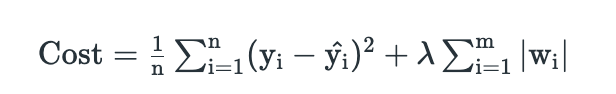
2. Ridge Regularization – L2 Regularization

A regression model that uses the L2 regularization technique is called Ridge regression. Ridge regression adds the “squared magnitude” of the coefficient as a penalty term to the loss function(L).

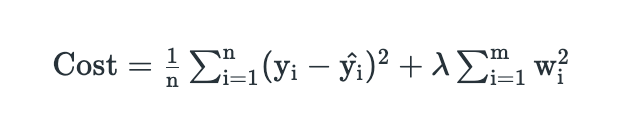
3. Elastic Net Regression

This model is a combination of L1 as well as L2 regularization. That implies that we add the absolute norm of the weights as well as the squared measure of the weights. With the help of an extra hyperparameter that controls the ratio of the L1 and L2 regularization.

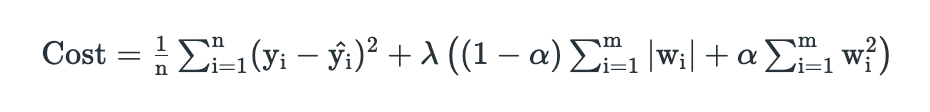
The main intuitive difference between the L1 and L2 regularization is that L1 regularization tries to estimate the median of the data while the L2 regularization tries to estimate the mean of the data to avoid overfitting.

t L1 regularization helps in feature selection by eliminating the features that are not important. If you have 2 extremely correlated features, you will get more understandable results with L2 regression because the coefficients will be quite evenly distributed among the features. If you use L1, you can get coefficients that differ greatly in magnitude even though they will probably be directionally the same.